Картинки названия геометрических фигур для детей
Удивительный мир геометрических фигур! Давайте начнем изучать основы геометрии с этих чудесных картинок для детей с названиями. Уже в три года названия геометрических фигур постепенно вводят в активный словарь детей. Фигуры бывают разные: плоскостные и объемные. Фигуры простейшие изучают в математике в начальной школе: они могут состоять из отрезков и замкнутых линий. А планиметрию и стереометрию проходят в более старших классах. Желаем, чтобы знакомство с геометрическими фигурами приносило детям радость. Ну, что ж, приступим…
 Этот удивительный мир геометрических фигур!
Этот удивительный мир геометрических фигур!
 Плоскостные геометрические фигуры
Плоскостные геометрические фигуры
 Объемные геометрические фигуры
Объемные геометрические фигуры
 Из таких фигур можно строить замки!
Из таких фигур можно строить замки!
 Простейшие (основные) геометрические фигуры
Простейшие (основные) геометрические фигуры
 Геометрические фигуры на плоскости
Геометрические фигуры на плоскости
 Какие геометрические фигуры изучают планиметрия и стереометрия
Какие геометрические фигуры изучают планиметрия и стереометрия
 Виды фигур на плоскости
Виды фигур на плоскости
 Криволинейные треугольники
Криволинейные треугольники
 Круг
Круг  Овал
Овал  Квадрат
Квадрат  Прямоугольник
Прямоугольник
 Овал и эллипс похожи, но различия есть
Овал и эллипс похожи, но различия есть
 Трапеция
Трапеция  Ромб
Ромб  Четырехугольник
Четырехугольник  Параллелограмм
Параллелограмм
 Правильные многоугольники
Правильные многоугольники
 Треугольник
Треугольник  Различные виды треугольников
Различные виды треугольников
 Куб
Куб
 Шар
Шар
 Цилиндр
Цилиндр
 Конус
Конус
 Пирамида
Пирамида
 Параллелепипед
Параллелепипед
 Призма
Призма
 Различные виды призм
Различные виды призм
 Усеченный конус
Усеченный конус
 Усеченная пирамида
Усеченная пирамида
 Правильные многогранники
Правильные многогранники
 Октаэдр
Октаэдр
 Икосаэдр
Икосаэдр
 Додекаэдр
Додекаэдр
|
Трапеция
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна \(180^\circ\).
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
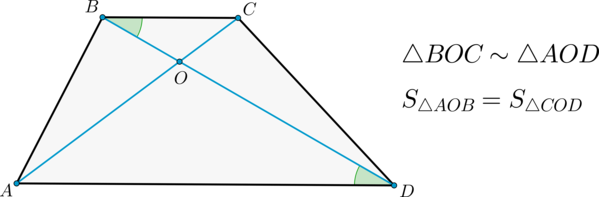
Доказательство
1) Т.к. \(AD\parallel BC\), то углы \(\angle BAD\) и \(\angle ABC\) – односторонние при этих прямых и секущей \(AB\), следовательно, \(\angle
BAD
+\angle ABC=180^\circ\).
2) Т.к. \(AD\parallel BC\) и \(BD\) – секущая, то \(\angle DBC=\angle
BDA\) как накрест лежащие.
Также \(\angle BOC=\angle AOD\) как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\).
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\). Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}\). Тогда: \[S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle
COD}\]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
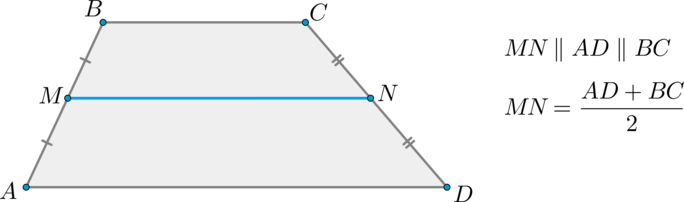
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
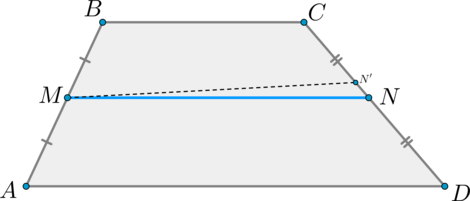
Проведем через точку \(M\) прямую \(MN’\parallel AD\) (\(N’\in CD\)). Тогда по теореме Фалеса (т.к. \(MN’\parallel AD\parallel BC, AM=MB\)) точка \(N’\) — середина отрезка \(CD\). Значит, точки \(N\) и \(N’\) совпадут.
2) Докажем формулу.
Проведем \(BB’\perp AD, CC’\perp AD\). Пусть \(BB’\cap MN=M’, CC’\cap
MN=N’\).
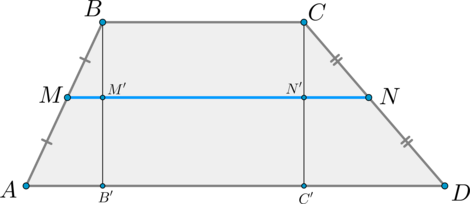
Тогда по теореме Фалеса \(M’\) и \(N’\) — середины отрезков \(BB’\) и \(CC’\) соответственно. Значит, \(MM’\) – средняя линия \(\triangle
ABB’\), \(NN’\) — средняя линия \(\triangle DCC’\). Поэтому: \[MM’=\dfrac12 AB’, \quad NN’=\dfrac12 DC’\]
Т.к. \(MN\parallel AD\parallel BC\) и \(BB’, CC’\perp AD\), то \(B’M’N’C’\) и \(BM’N’C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B’M’=M’B\). Значит, \(B’M’N’C’\) и \(BM’N’C\) – равные прямоугольники, следовательно, \(M’N’=B’C’=BC\).
Таким образом:
\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
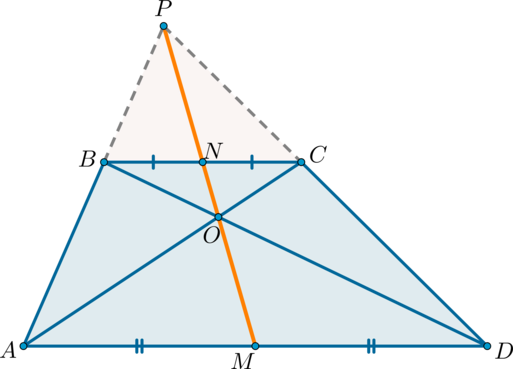
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\), \(N\) и \(M\) лежат на одной прямой.
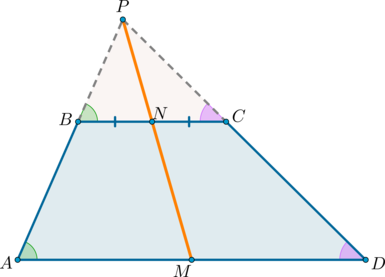
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\)). Пусть она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
Рассмотрим \(\triangle BPN\) и \(\triangle APM\). Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\). Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\). Но \(BN=NC\), следовательно, \(AM=DM\).
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
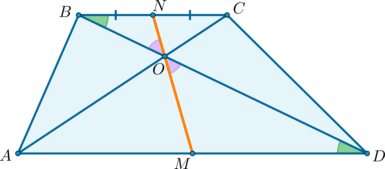
Пусть \(N\) – середина \(BC\), \(O\) – точка пересечения диагоналей. Проведем прямую \(NO\), она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle
ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\). Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\). Но \(BN=CN\), следовательно, \(AM=MD\).
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\).
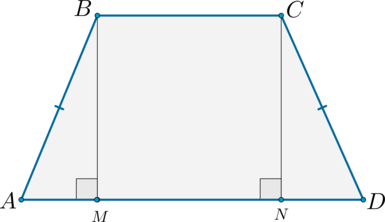
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\), то \(BM\parallel CN\); \(AD\parallel BC\), тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\).
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\). Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\), то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\).
2) 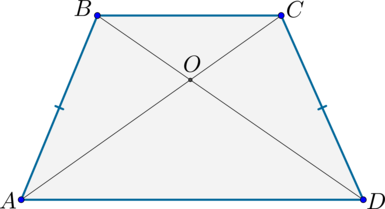
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку \(\triangle ABD=\triangle ACD\). Следовательно, \(AC=BD\).
3) Т.к. \(\triangle ABD=\triangle ACD\), то \(\angle BDA=\angle CAD\). Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\), такую что \(\angle A = \angle D\).
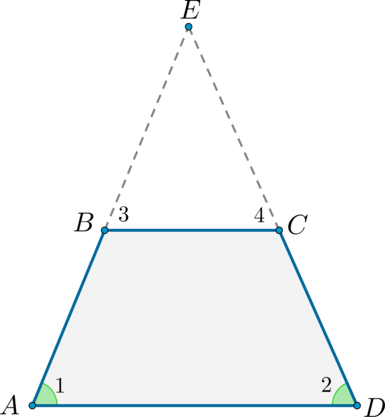
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\), то треугольник \(AED\) равнобедренный и \(AE
= ED\). Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\). Аналогично равны углы \(2\) и \(4\), но \(\angle 1 = \angle 2\), тогда \(\angle 3 = \angle 1 = \angle 2 =
\angle 4\), следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\).
В итоге \(AB = AE — BE = DE — CE = CD\), то есть \(AB = CD\), что и требовалось доказать.
2) Пусть \(AC=BD\). Т.к. \(\triangle AOD\sim \triangle BOC\), то обозначим их коэффициент подобия за \(k\). Тогда если \(BO=x\), то \(OD=kx\). Аналогично \(CO=y \Rightarrow AO=ky\).
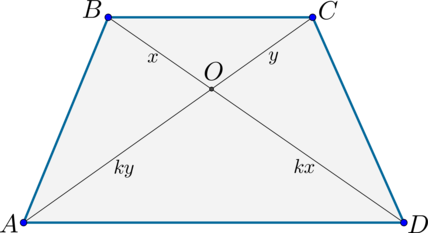
Т.к. \(AC=BD\), то \(x+kx=y+ky \Rightarrow x=y\). Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\).
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\), чтд.
Плоские геометрические фигуры: свойства и основные формулы
В статье дается определение, основные свойства и формулы для следующих геометрических фигур:
Четырёхугольник
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Основные свойства:
- Сумма углов четырёхугольника равна 360°
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
- Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Квадрат
Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Основные формулы:
Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a2или S=d2/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2
где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.
Свойства:
- Все стороны равны, все углы равны и составляют 90°;
- Диагонали квадрата равны и перпендикулярны;
- У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
- Квадрат является одновременно частным случаем ромба и прямоугольника.
Прямоугольник
Прямоугольник — четырехугольник, у которого все углы прямые.
Основные формулы:
Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a2+b2)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a2+b2)/2 (теорема Пифагора)
где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a2+b2) – корень квадратный из (a2+b2).
Свойства:
- Диагонали прямоугольника равны и делятся точкой пересечения пополам.
- Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Параллелограмм
Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Определения:
Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Основные формулы:
Стороны и диагональ связаны соотношением: (d1)2+(d2)2=(a2+b2)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
Площадь по двум сторонам и углу между ними: S=a*b*sin α
Площадь по двум диагоналям и углу между ними: S=(d1*d2)/2*sin γ
где a, b — длины сторон, d1, d2 –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).
Свойства:
- У параллелограмма противоположные стороны равны и противоположные углы равны.
- Сумма любых двух соседних углов параллелограмма равна 180°.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
- Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Основные формулы:
Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d1*d2)/2
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a2 · sin α
Радиус окружности, вписанной в ромб: r=h/2 или r =(d1*d2)/4a
где a — длина стороны, d1, d2 –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба
Свойства:
- Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
- В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d1*d2/4a.
Трапеция
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Определения:
- Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
- Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
- Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
- Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
- Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
- Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Основные формулы:
Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2
где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d1, d2 –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне
Свойства:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
Треугольник
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Определения:
- Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
- Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
- Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
- Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь по сторонам и углу между ними: S=(a*b)/2* sin γ
Площадь по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
Площадь по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d1, d2 –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности
Свойства:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Сумма углов треугольника равна 180°:
- Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
- Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
- Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
- В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
- Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.
Определения:
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
- Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
- Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
- Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
- Секущая — прямая, которая пересекает окружность в двух различных точках.
Основные формулы:
Длина окружности: L = 2πR
Площадь круга: S = π*r2 или S = π*d2/4
где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.
Трапеция — это… Что такое Трапеция?
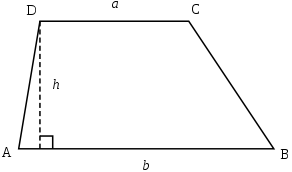
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Две параллельные стороны называются основанием трапеции, а две другие — это боковые стороны. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.
Связанные определения
Элементы трапеции
- Параллельные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
Виды трапеций
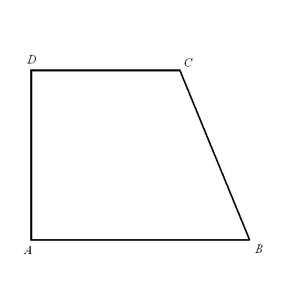
Прямоугольная трапеция
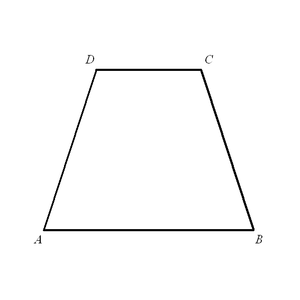
Равнобедренная трапеция
- Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной.
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Общие свойства
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей, равен полуразности оснований.
- (Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
Свойства и признаки равнобедренной трапеции
- Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
- Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
- В равнобедренной трапеции углы при любом основании равны.
- В равнобедренной трапеции длины диагоналей равны.
- Если трапецию можно вписать в окружность, то она равнобедренная.
- Около равнобедренной трапеции можно описать окружность.
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная и описанная окружность
Площадь
- Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.
- В случае, если и — основания и — высота, формула площади:
- В случае, если — средняя линия и — высота, формула площади:
ɴʙ Эти формулы — одинаковы, так как полусумма оснований равняется средней линии трапеции:
- Формула, где , — основания, и — боковые стороны трапеции:
- Площадь равнобедренной трапеции с радиусом вписанной окружности, равным , и углом при основании :
- В частности, если угол при основании равен 30°, то:
- .
См. также
Примечания
трапеция — Trapezoid — qwe.wiki
В евклидовой геометрии , A выпуклая четырехугольная с , по меньшей мере , одной пары параллельных сторон, называется как трапеции ( т г æ р ə г ɔɪ г / ) в американском и канадском английском , но в качестве трапеции ( ) на английском языке за пределами Северной Америки. Параллельные стороны называются основания трапеции , а две другие стороны называются ноги или боковые стороны (если они не параллельны, в противном случае есть две пары оснований). Неравносторонним трапеции является трапецией с не сторонами равной меры, в отличие от частных случаев ниже.
Этимология
Термин трапеция была в использовании на английском языке с 1570 года, от поздней латинской трапеции , от греческого τραπέζιον ( trapézion ), буквально «столика», уменьшительный от τράπεζα ( Трапезы ), « за стол», который сам из τετράς ( тетр ) , «четыре» + πέζα ( Пеза ), «нога, конец, граница, край».
Первое зарегистрированное использование греческого слова в переводе трапеции (τραπεζοειδή, trapezoeidé , «Таблицеподобный») было на Маринусе Прокл (412 до 485 н.э.) в своем комментарии на первую книгу Евклида .
В данной статье используется термин трапеции в том смысле , что является текущим в Соединенных Штатах и Канаде. Во многих других языках , использующих слово происходит от греческого на эту фигуру, формы , наиболее близкой к трапеции (например , португальский trapézio , французские трапеции , итальянский trapezio , испанский trapecio , немецкий Trapez , русская «трапеция») используются.
Инклюзивное против исключительного определения
Существует некоторое разногласие ли параллелограммы , у которых есть две пары параллельных сторон, следует рассматривать как трапеции. Некоторые определяют трапецию как четырехугольник , имеющий только одну пару параллельных сторон (исключительное определение), тем самым исключая параллелограммы. Другие определяют трапецию как четырехугольник с по меньшей мере одной пары параллельных сторон (инклюзивное определение), что делает параллелограмм особый вид трапеции. Последнее определение согласуется с его использования в высшей математике , таких как исчисление . Первое определение было бы сделать такие понятия , как приближение трапециевидного к определенному интегралу плохо определен. В этой статье используется широкое определение и рассматривает параллелограммы как частные случаи трапеции. Это также выступает в систематике четырехугольников .
Под широким определением, все параллелограммы (включая ромбы , прямоугольники и квадраты ) являются трапеции. Прямоугольники имеют зеркальную симметрию по середине ребер; ромбы имеют зеркальную симметрию на вершинах, а квадраты имеют зеркальную симметрию с обеих средних ребер и вершин.
Особые случаи
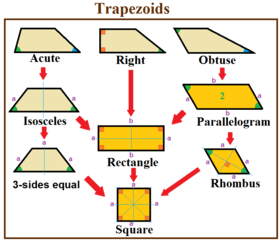
Трапециевидные особые случаи. Оранжевые цифры также квалифицируются как параллелограммы.
Правая трапеция (также называется прямоугольная трапеция ) имеет два смежных прямые углов . Правый трапеции используются в трапеций для оценки площади под кривой.
Острой трапеции имеет два смежных острых углов на его более длинной базовой кромке, в то время как тупые трапеции имеет один острый и один тупой угол на каждой базе .
Равнобедренной трапеции является трапецией , где стороны (ноги) имеют одинаковую длину, а углы основания имеют одинаковую меру. Она имеет симметрию отражения . Это возможно при острых или правильных трапеций.
Параллелограмм является трапеция с двумя парами параллельных сторон. Параллелограмм имеет центральную 2-кратную осевую симметрию (или отражение точки симметрии). Можно для тупых или правой трапеции.
Тангенциальная трапеция является трапецией , которая имеет вписанную .
Саккери четырехугольник похож на трапецию в гиперболической плоскости, с двумя соседними прямыми углами, в то время как он представляет собой прямоугольник , в евклидовой плоскости. Ламберт четырехугольник в гиперболической плоскости имеет 3 прямых углов.
Состояние существования
Четыре длина , с , б , д может составлять последовательную стороны не-параллелограмма трапеции с и б параллельны только тогда , когда
- |d-с|<|б-a|<d+с,{\ Displaystyle \ displaystyle | DC | <| ба | <d + с.}
Четырехугольник является параллелограммом , когда , но это экс-тангенциального четырехугольник (который не является трапеция) , когда .
d-сзнак равноб-aзнак равно0{\ Displaystyle DC = Ьа = 0}|d-с|знак равно|б-a|≠0{\ Displaystyle | DC | = | ба | \ NEQ 0}
характеризации
Учитывая выпуклый четырехугольник, следующие свойства эквивалентны, и каждая предполагает, что четырехугольник является трапецией:
- Она состоит из двух смежных углов , которые являются дополнительными , то есть, они добавляют до 180 градусов .
- Угол между стороной и диагональю равен углу между противоположной стороной и той же диагональю.
- В диагоналях рубят друг друг во взаимно же соотношении (это отношение такого же , как между длинами параллельных сторон).
- Диагонали разрезать четырехугольник на четыре треугольника, одна из которых противоположны пар похожи .
- Диагонали разрезать четырехугольник на четыре треугольника, одна из которых противоположны паров имеют равные площади.
- Произведение площадей двух треугольников, образованных одной диагонали равна произведению площадей двух треугольников, образованных другой диагонали.
- Области S и T некоторых двух противоположных треугольников четырех треугольников , образованных диагоналями удовлетворяют уравнению
- Кзнак равноS+T,{\ Displaystyle {\ SQRT {К}} = {\ SQRT {S}} + {\ SQRT {T}}}
- где K является площадь четырехугольника.
- Середины двух противоположных сторон и пересечение диагоналей коллинеарны .
- Углы в четырехугольнике ABCD удовлетворяют условиюгрехAгрехСзнак равногрехВгрехD,{\ Displaystyle \ грех А \ грех С = \ грех В \ грех Д.}
- Косинусы двух смежных углов просуммировать 0, как это делают косинусы двух других углов.
- В котангенсах двух смежных углов просуммировать 0, как это делают котангенсы двух других смежных углов.
- Один bimedian делит четырехугольник на два четырехугольника равных областей.
- Дважды длина bimedian, соединяющей средние точки двух противоположных сторон равна сумме длин других сторон.
Кроме того, следующие свойства эквивалентны, и каждая предполагает , что противоположные стороны и б параллельны:
- Последовательные стороны , с , б , д и диагоналей р , д удовлетворяют уравнению
- п2+Q2знак равнос2+d2+2aб,{\ Displaystyle р ^ {2} + д ^ {2} = с ^ {2} + й ^ {2} + 2ab.}
- Расстояние V между серединами диагоналей удовлетворяет уравнению
- vзнак равно|a-б|2,{\ Displaystyle v = {\ гидроразрыва {| AB |.} {2}}}
Midsegment и высота
Midsegment (также называемый средней или срединный) трапеции является сегментом , который присоединяется к срединным ножкам. Это параллельно основаниям. Его длина м равна среднему значению длин оснований а и б трапеции,
- мзнак равноa+б2,{\ Displaystyle т = {\ гидроразрыва {а + Ь} {2}}.}
Midsegment трапеции является одним из два bimedians (другой bimedian делит трапецию на равные области).
Высота (или высота) является перпендикулярным расстоянием между основаниями. В случае, когда обе основы имеют разную длину ( ≠ б ), высота трапеции ч может быть определена по длине его четырех сторон , используя формулу
- часзнак равно(-a+б+с+d)(a-б+с+d)(a-б+с-d)(a-б-с+d)2|б-a|{\ Displaystyle ч = {\ гидроразрыва {\ SQRT {(-a + B + C + D) (аb + C + D) (AB + CD) (AB-C + D)}} {2 | ба |}}}
где с и d являются длины ног.
Площадь
Площадь К трапеции задается
- Кзнак равноa+б2⋅часзнак равномчас{\ Displaystyle К = {\ гидроразрыва {а + Ь} {2}} \ CDOT ч = тк}
где и б являются длины параллельных сторон, ч является высота (перпендикулярное расстояние между этими сторонами), и т представляет собой среднее арифметическое длин двух параллельных сторон. В 499 AD Aryabhata , великий математик — астроном из классического возраста индийской математики и индийской астрономии , использовал этот метод в Aryabhatiya (раздел 2.8). Это дает как частный случай хорошо известную формуле для площади треугольника , рассматривая треугольник как вырожденные трапеции , в котором одна из параллельных сторон сократились до точки.
Индийский математик 7-го века Бхаскара I вывел следующую формулу для площади трапеции с последовательными сторонами , с , б , д :
- Кзнак равно12(a+б)с2-14((б-a)+с2-d2б-a)2{\ Displaystyle К = {\ гидроразрыва {1} {2}} (а + б) {\ SQRT {с ^ {2} — {\ гидроразрыва {1} {4}} \ влево ((ба) + {\ гидроразрыва {с ^ {2} -d ^ {2}} {ба}} \ справа) ^ {2}}}}
где и б параллельны и б > . Эта формула может быть разложена на более симметричную версию
- Кзнак равноa+б4|б-a|(-a+б+с+d)(a-б+с+d)(a-б+с-d)(a-б-с+d),{\ Displaystyle К = {\ гидроразрыва {а + Ь} {4 | ба |}} {\ SQRT {(-a + B + C + D) (а-Ь + с + d) (а-б + CD) (AB-C + d)}}.}
Когда одна из параллельных сторон сократились до точки (скажу = 0), то эта формула сводится к формуле Герона для площади треугольника.
Другая эквивалентная формула для области, которая более близко напоминает формулу Герона, является
- Кзнак равноa+б|б-a|(s-б)(s-a)(s-б-с)(s-б-d),{\ Displaystyle К = {\ гидроразрыва {а + Ь} {| ба |}} {\ SQRT {(SB) (са) (SBC) (SBD)}}}
где это -полупериметр трапеции. (Эта формула аналогична формуле Брахмагуптов , но отличается от него, в том , что трапеция не может быть циклической (вписанными в окружности). Формула также частный случай формулы Бретшнейдера для общего четырехугольника ).
sзнак равно12(a+б+с+d){\ Displaystyle s = {\ tfrac {1} {2}} (A + B + C + D)}
Из формулы Бретшнейдера, отсюда следует, что
- Кзнак равно(aб2-a2б-ad2+бс2)(aб2-a2б-aс2+бd2)(2(б-a))2-(б2+d2-a2-с24)2,{\ Displaystyle К = {\ SQRT {{\ гидроразрыва {(аб ^ {2} -a ^ {2} Ь-ад ^ {2} + BC ^ {2}) (аб ^ {2} -a ^ {2 } Ь-ас ^ {2} + шд ^ {2})} {(2 (ба)) ^ {2}}} — \ влево ({\ гидроразрыва {Ь ^ {2} + й ^ {2} -a ^ {2} -с ^ {2}} {4}} \ справа) ^ {2}}}.}
Линия, которая соединяет Середины параллельных сторон, рассекает область.
Диагонали
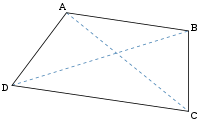
Длины диагоналей
- пзнак равноaб2-a2б-aс2+бd2б-a,{\ Displaystyle р = {\ SQRT {\ гидроразрыва {аб ^ {2} -a ^ {2} Ь-ас ^ {2} + шд ^ {2}} {ба}}}}
- Qзнак равноaб2-a2б-ad2+бс2б-a{\ Displaystyle д = {\ SQRT {\ гидроразрыва {аб ^ {2} -a ^ {2} Ь-ад ^ {2} + BC ^ {2}} {ба}}}}
где является коротким основанием, б является длительным основанием, и с и d являются трапециевидными ногами.
Если трапеция делится на четыре треугольника его диагоналей AC и BD (как показано справа), пересекающихся в O , то площадь AOD равно , что из ВОС , и продукт из областей AOD и BOC равна к тому , что из а и COD . Отношение площадей каждой пары смежных треугольников такое же , как между длинами параллельных сторон.
△{\ Displaystyle \ треугольник} △{\ Displaystyle \ треугольник} △{\ Displaystyle \ треугольник} △{\ Displaystyle \ треугольник} △{\ Displaystyle \ треугольник} △{\ Displaystyle \ треугольник}
Пусть трапеция имеют вершины A , B , C и D в последовательности и имеют параллельные стороны AB и DC . Пусть Е пересечение диагоналей, и пусть F быть на стороне DA и G быть на стороне до н.э. таким образом, что FEG параллельна AB и CD . Тогда FG является гармоническое среднее из AB и DC :
- 1Fгзнак равно12(1AВ+1DС),{\ Displaystyle {\ гидроразрыва {1} {ФГ}} = {\ гидроразрыва {1} {2}} \ влево ({\ гидроразрыва {1} {АВ}} + {\ гидроразрыва {1} {DC}} \ вправо ).}
Линия, которая проходит через обе точки пересечения расширенных непараллельных сторон и точки пересечения диагоналей, делит пополам каждую базу.
Другие свойства
Центр области (центр массы для равномерного пластинки ) лежит вдоль отрезка , соединяющего середин параллельных сторон, при перпендикулярном расстоянии х от более длинной стороны б задается
- Иксзнак равночас3(2a+бa+б),{\ Displaystyle х = {\ гидроразрыва {ч} {3}} \ влево ({\ гидроразрыва {2а + Ь} {а + Ь}} \ справа).}
Центр области делит этот отрезок в соотношении (когда взято от короткого замыкания на длинную сторону)
- a+2б2a+б,{\ Displaystyle {\ гидроразрыва {а + 2b} {2a + Ь}}.}
Если угол биссектрисы до углов A и B пересекаются в точке P , а угловые биссектрисы к углам С и D пересекаются в точке Q , то
- пQзнак равно|AD+ВС-AВ-СD|2,{\ Displaystyle PQ = {\ гидроразрыва {| AD + BC-AB-CD |.} {2}}}
Подробнее о терминологии
Термин трапеция была однажды определили как четырехугольник без параллельных сторон в Великобритании и в других странах. (Оксфордский словарь английского языка говорит : «Часто называют английскими писателями в 19 веке».) В соответствии с Оксфордский словарь английского языка , в смысле фигуры без каких — либо сторон параллельна смысл , для которого Прокл ввел термин «трапеция». Это сохраняется во французском trapézoïde (), немецкий Трапецоида , и на других языках. Тем не менее, именно этот смысл считается устаревшим.
Трапеции в смысле Прокла четырехугольник , имеющий одну пару его противоположных сторон параллельно. Это был конкретный смысл в Англии в 17 — м и 18 — м веках, и вновь превалирует один в последнее время использования за пределами Северной Америки. Трапеция как любой четырехугольник более общего , чем параллелограмм смысл этого термина в Евклиде .
Смутно, слово трапеции иногда используется в Англии из с. 1800 -с. 1875, для обозначения нерегулярных четырехугольник, не имеющего стороны не параллельны друг другу. Это является устаревшим в Англии, но по- прежнему в Северной Америке. Однако эта форма более обычно (и меньше смешения) просто называют нерегулярный четырехугольник.
Приложения

Архитектура
В архитектуре это слово используется для обозначения симметричных дверей, окон, а также здания построено шире у основания, сужающиеся к вершине, в египетском стиле. Если они имеют прямые стороны и острые угловые углы, их форма, как правило равнобедренные трапеции . Это был стандартный стиль для дверей и окон Инка .
Геометрия
Пересекла проблема лестницы является проблемой нахождения расстояния между параллельными сторонами прямоугольной трапеции, учитывая диагональные длины и расстояние от перпендикулярной ноги к диагональному пересечению.
Биология

В морфологии , систематике и других описательных дисциплинах , в которых термин для таких форм необходим, термины , таких как трапециевидные или трапециевидные обычно являются полезными в описаниях конкретных органов или форм.
Смотрите также
Рекомендации
дальнейшее чтение
внешняя ссылка
Свойства трапеции
Определения и формулы для периметра трапеции, площади трапеции, свойств сторон и углов трапеции, свойств сторон и углов равнобедренной трапеции
Просто прокрутите вниз или нажмите на то, что вы хотите, и я прокручу для вас!
| Периметр трапеции: | |
| Чтобы найти периметр трапеции, просто сложите все длины сторон: Периметр = a + b + c + B |
| |
| Площадь трапеции: | |
| Найти площадь трапеции… Более длинное основание (нижнее) — это большая B, а меньшее основание (верхнее) — это маленькая b … |
| Да, вот формула … Но давайте посмотрим, откуда она взялась! | |
Возьмите две копии трапеции (одну синюю трапецию и одну зеленую трапецию) … Переверните одну вверх ногами и склейте их вместе … Теперь у вас есть параллелограмм. Площадь параллелограмма = основание x высота Но это вдвое больше, чем нам нужно… Итак, умножаем на 1/2! |

,
| 1D линия 2D правильных многоугольников: равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, нонагон, десятиугольник, шестиугольник, двенадцатигранник, шестиугольник, N-угольник, многоугольник кольцо другие многоугольники: 90 004 Круглые формы: 3D архимедова Solids: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: 4Д | Anzeige Расчеты на правой трапеции (или правой трапеции).Это трапеция с двумя смежными прямыми углами. Введите длины двух параллельных сторон a и c, а также основания b или наклонной стороны d. Выберите количество десятичных знаков и нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы. Формулы: Длины сторон, диагонали и периметр имеют одинаковые единицы измерения (например,грамм. метр), площадь имеет эту единицу квадрата (например, квадратный метр). Anzeige Поделиться: © Jumk.de Webprojects Anzeige |
.
Площадь трапеции. Определение, формула и калькулятор
Площадь трапеции. Определение, формула и калькулятор — Открытый справочник по математике
Количество квадратных единиц, необходимое для полного заполнения
трапеции.
Формула: Средняя ширина × высота
Попробуйте это Перетащите оранжевые точки, чтобы переместить и изменить размер трапеции. Как размер трапеции
изменяется, пересчитывается площадь.
Формула площади
Площадь трапеции — это средняя ширина, умноженная на высоту, или формула:
где
b1, b2 — длины каждого основания
h — высота (высота)

Напомним, что основания — это две параллельные стороны трапеции.Высота (или высота) трапеции — это
перпендикулярное расстояние
между двумя базами.
В приведенном выше апплете нажмите «заморозить размеры». Когда вы перетаскиваете любую вершину, вы увидите, что трапеция перерисовывается, сохраняя неизменными высоту и основания. Обратите внимание, как область в отображаемой формуле не меняется. Площадь зависит только от высоты и длины основания, поэтому, как видите, существует множество трапеций с заданным набором размеров, которые имеют одинаковую площадь.
Вывод формулы
См. Как получить формулу площади трапеции.
Калькулятор
Используйте калькулятор выше, чтобы рассчитать высоту, базовую длину и площадь трапеции.
Введите любые три значения, и будет вычислено недостающее.
Например: введите высоту и две базовые длины и нажмите «Рассчитать». Площадь будет рассчитана.
Точно так же, если вы введете площадь и две длины основания, будет рассчитана высота, необходимая для получения этой площади.
Определение высоты по площади
Как найти высоту (высоту) трапеции, задайте две базы и площадь.Приведенная выше основная формула площади имеет четыре переменных (площадь, два основания и высота). Если мы знаем какие-то три, мы всегда можем найти четвертый.
Так, например, если мы знаем площадь и две базы, мы можем найти высоту, просто изменив основную формулу:
Где a — это площадь, а b1, b2 — две базы.
Поиск базы в районе
Как найти основание трапеции, укажите одно из оснований, высоту и площадь.
Приведенная выше основная формула площади имеет четыре переменных (площадь, два основания и высота).Если мы знаем какие-то три, мы всегда можем найти четвертый.
Так, например, если мы знаем площадь, одно основание и высоту, мы можем найти недостающее основание, просто изменив основную формулу:
Где a — площадь, b — известная база, а h — высота (высота).
Если известно медианное значение
 Напомним, что
Напомним, что
медиана (м) трапеции
— отрезок, соединяющий середины непараллельных сторон. Напомним также, что длина медианы — это среднее значение двух параллельных сторон.См. Медиана трапеции
Где м — это медиана, а ч — высота (высота).
Площадь как сложная форма
Другой способ найти площадь трапеции — рассматривать ее как несколько более простых форм, а затем добавлять или вычитать их площади, чтобы найти результат. Для
Например, трапецию можно рассматривать как меньший прямоугольник плюс два прямоугольных треугольника:
Дополнительные сведения об этой общей технике см. В разделе «Область неправильных многоугольников».
Координатная геометрия
В координатной геометрии, если вы знаете координаты четырех вершин,
вы можете рассчитать различные его свойства, в том числе площадь и периметр.Подробнее об этом см. Площадь и периметр трапеции (координатная геометрия).
Что попробовать
- На рисунке выше нажмите «скрыть детали»
- Перетащите оранжевые точки на вершинах, чтобы создать трапецию произвольного размера.
- Рассчитайте площадь по формуле
- Теперь попробуйте оценить площадь трапеции, просто глядя на
квадратов внутри нее. - Когда вы закончите, нажмите «Показать подробности», чтобы увидеть, насколько близко вы подошли.
Другие полигоны
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
,



